Moving mesh methods: Pictures and Animations
Most of the computations shown here were performed using the MMPDE moving mesh - linear finite
element method.
Click the pictures to see animations.
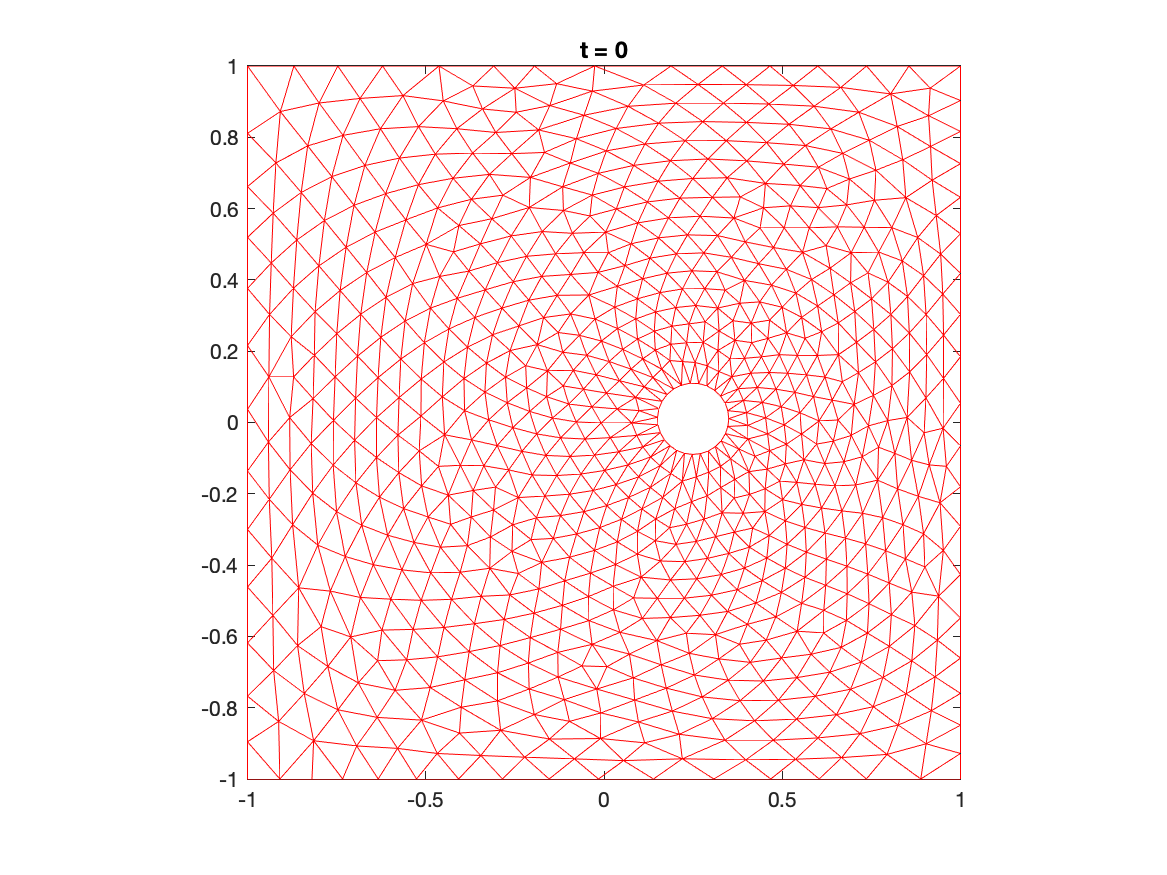
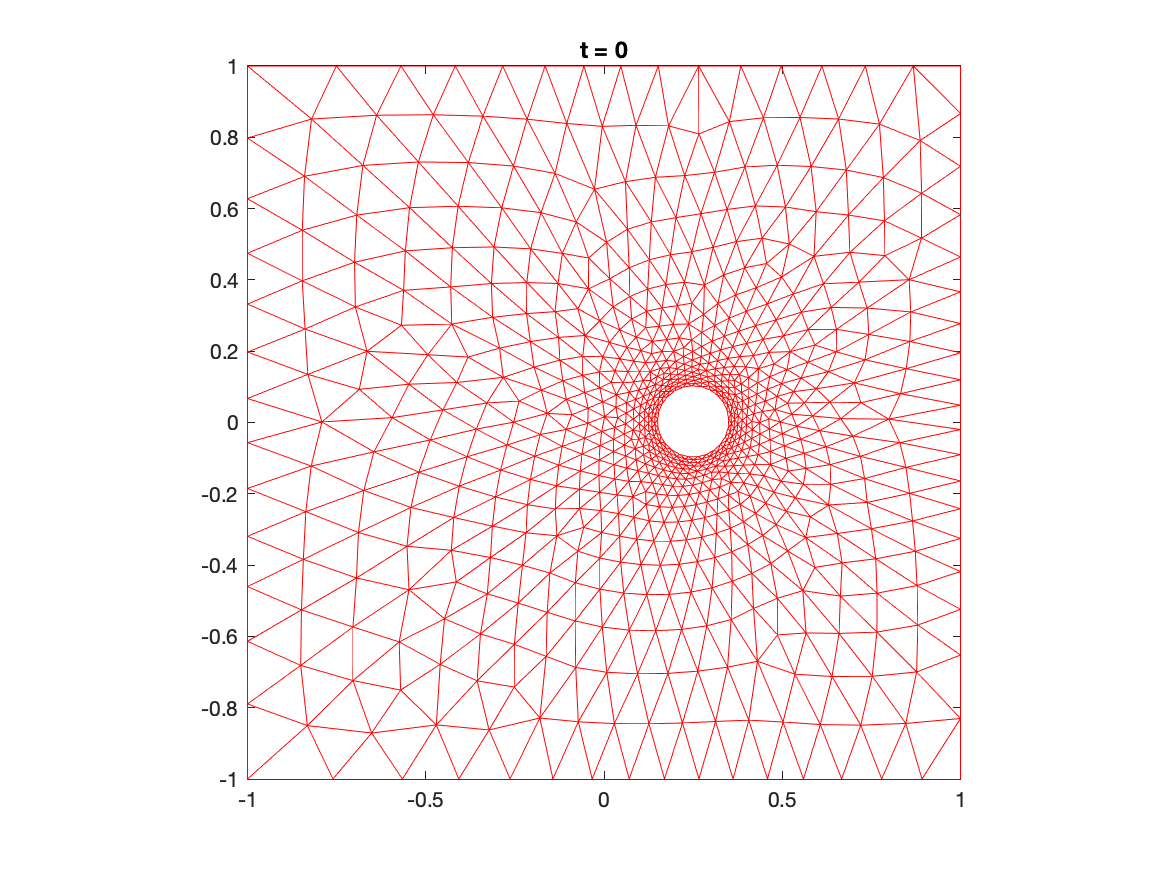
Moving meshes around a moving cylinder with or without concentration:
Burgers' equation:
1D: A mesh of 80 elements was used.
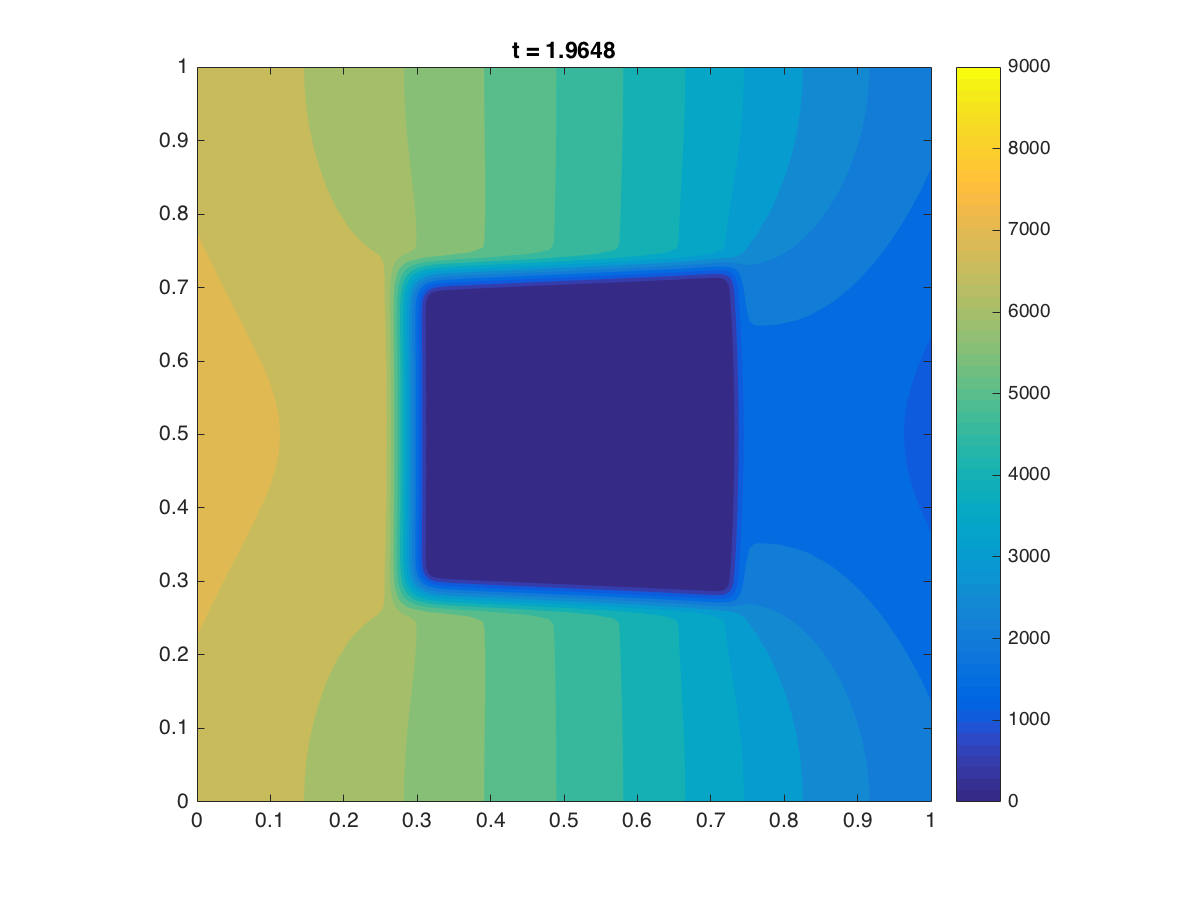
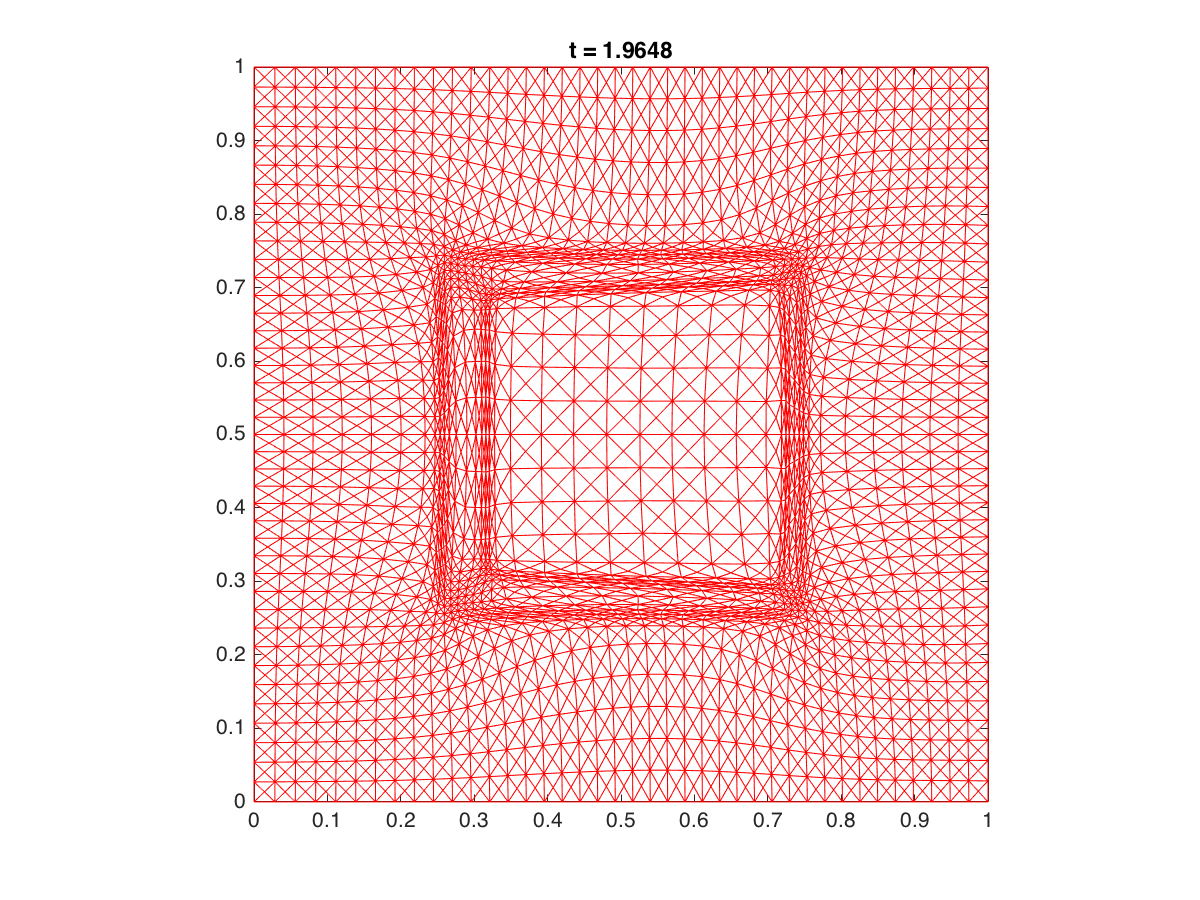
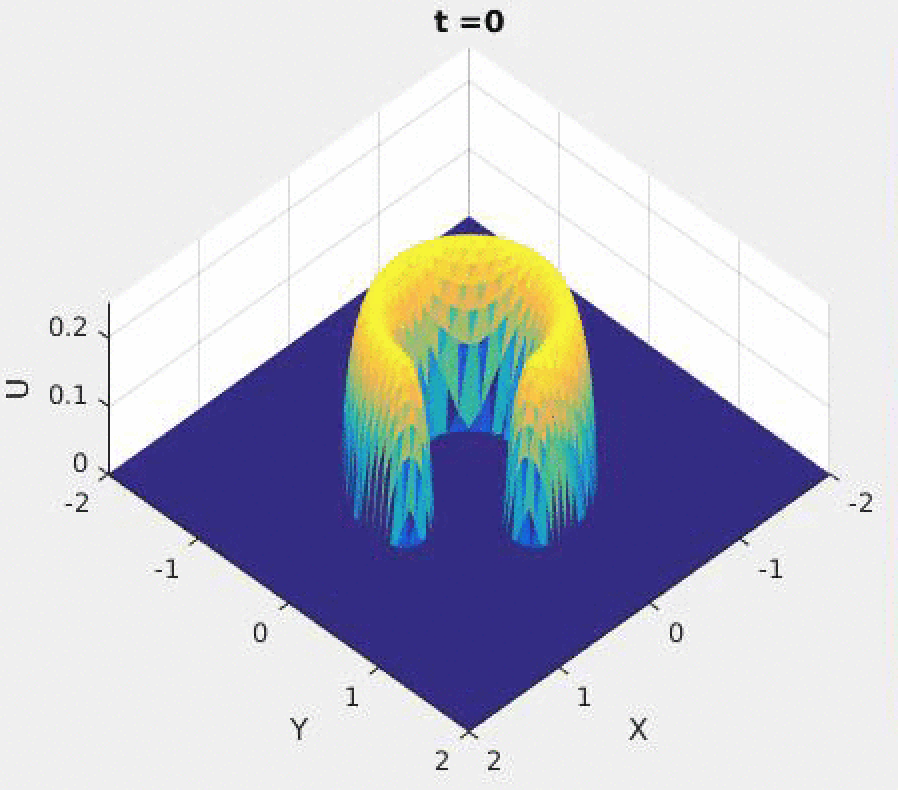
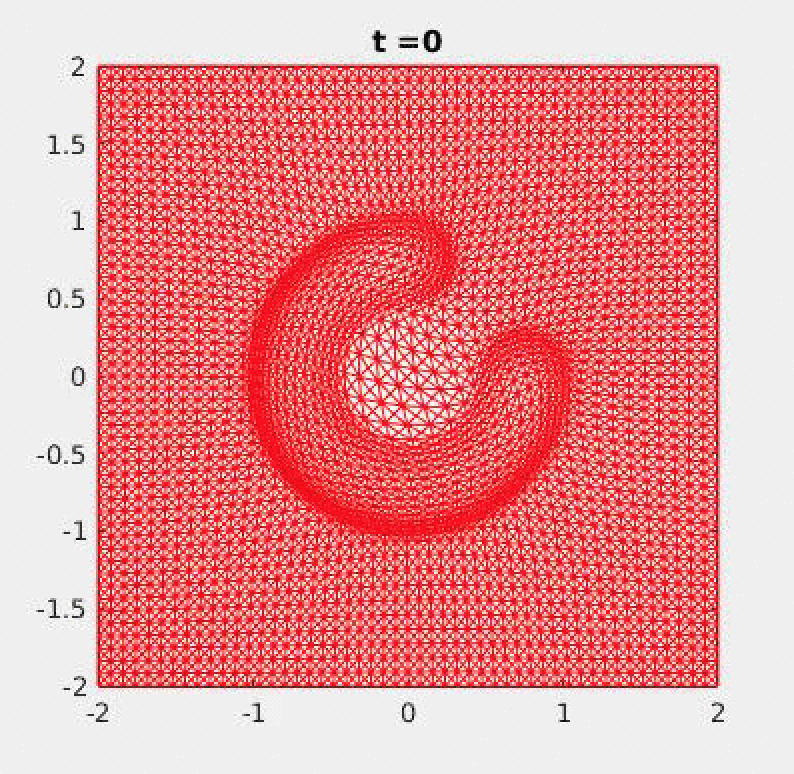
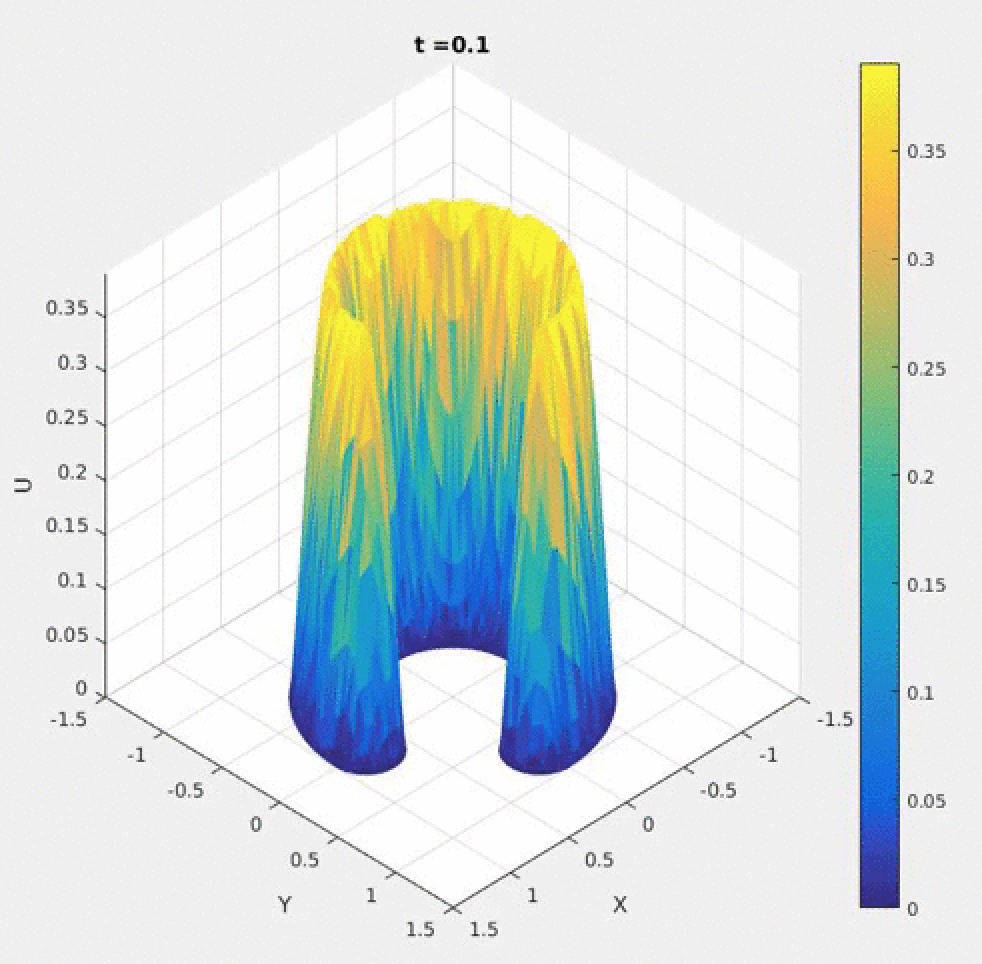
2D: A moving mesh of 3200 triangle elements with the two-level mesh movement strategy was used. The PDE
was solved on a finer mesh of 12800 elements.
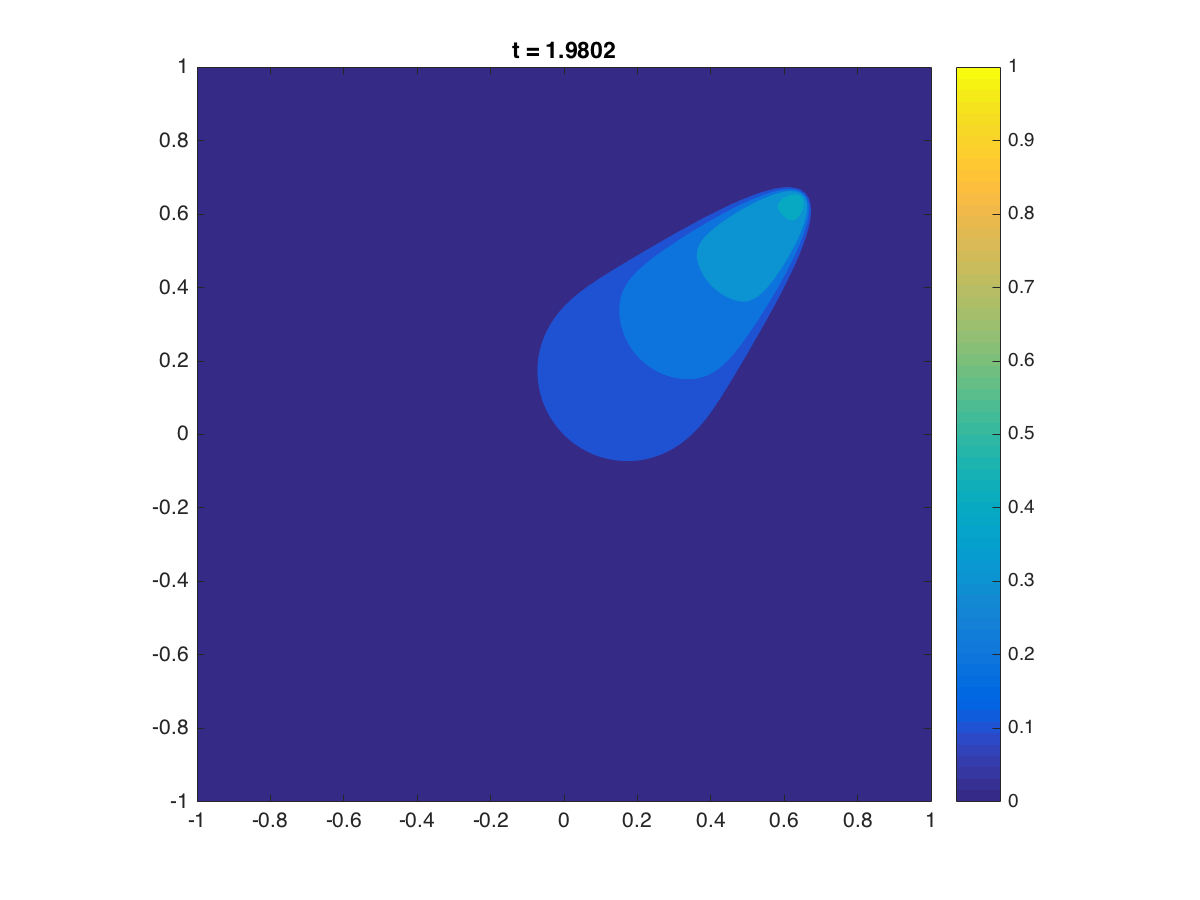
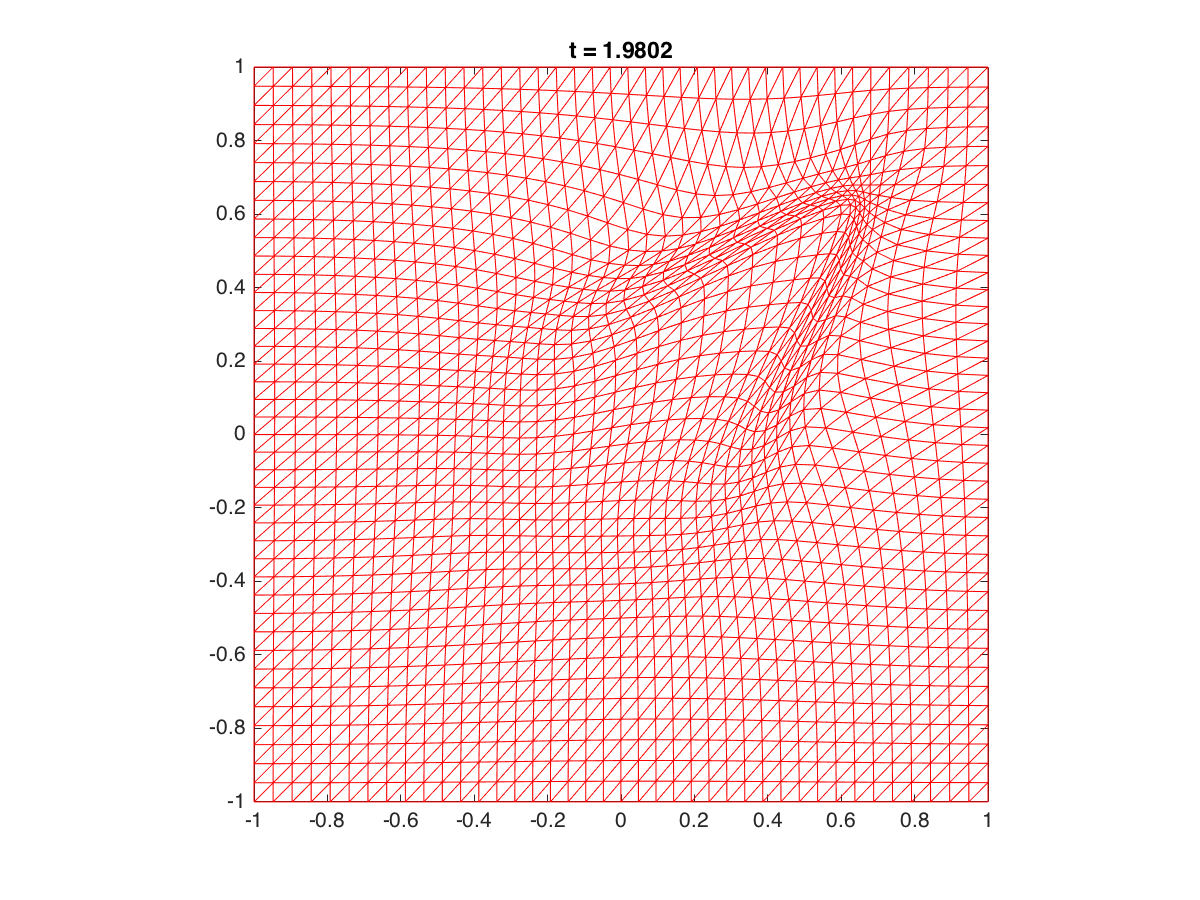
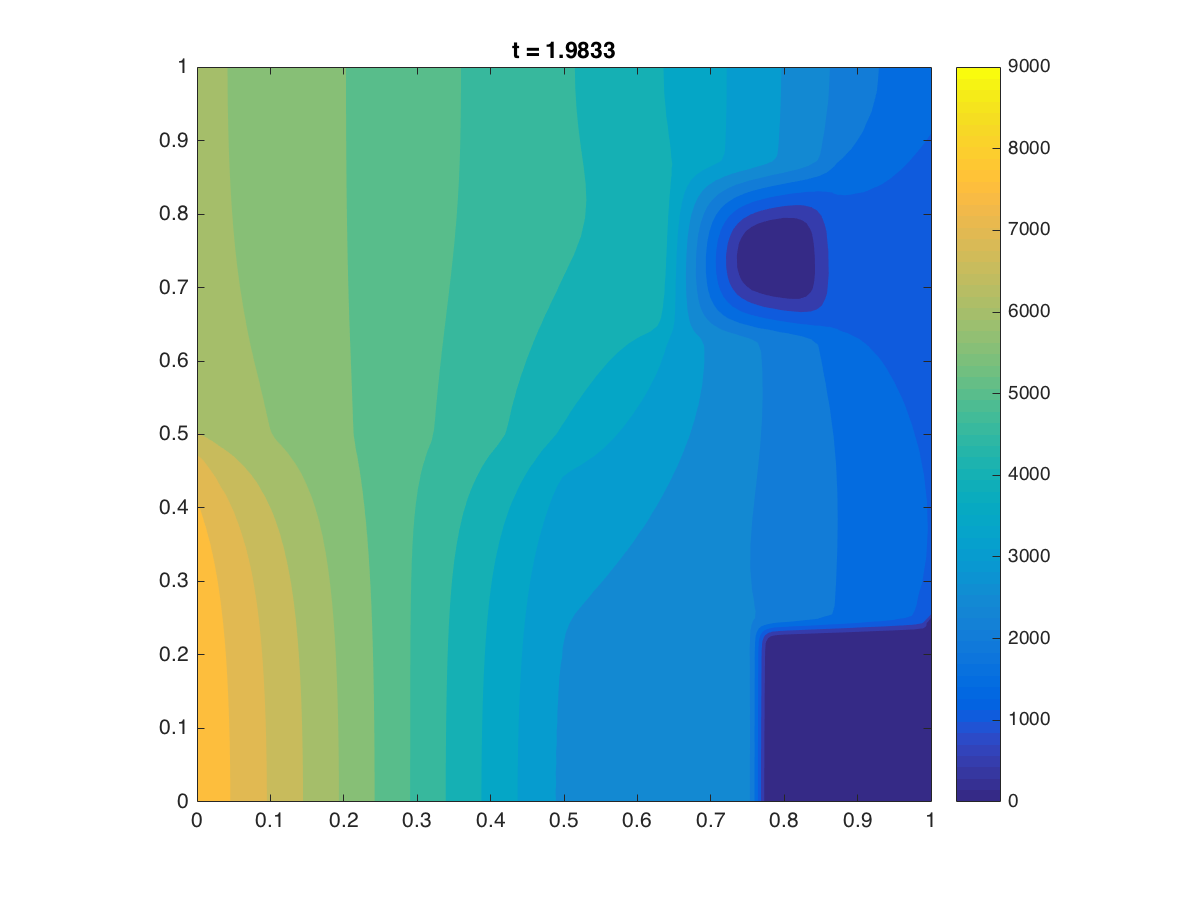
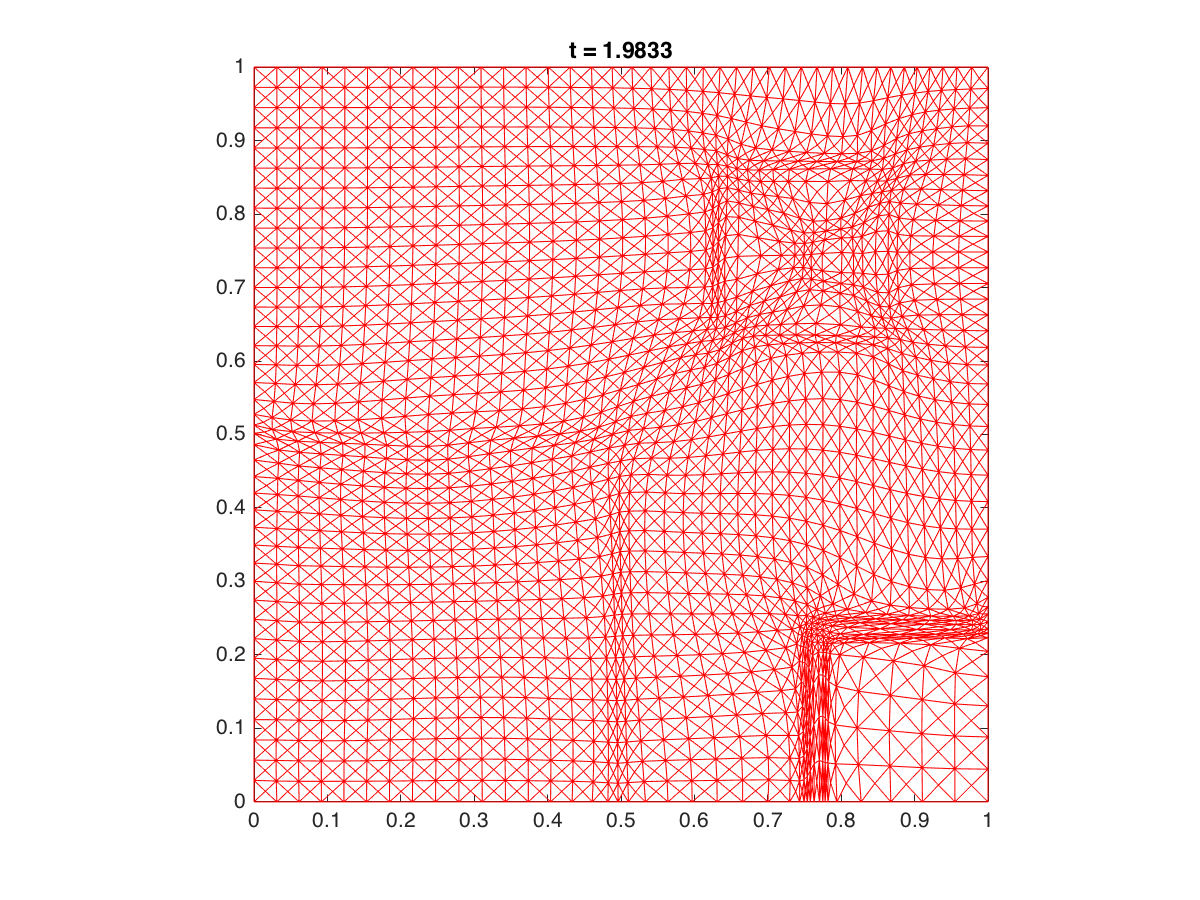
The radiation diffusion equation:
2D: A mesh of 6400 triangle elements was used. See, for instance, X. Yang et al.,
A moving mesh finite difference method for equilibrium radiation diffusion equations,
J. Comput. Phys. 298 (2015), 661-677 for the description of the (equilibrium) radiation-diffusion equation.
The Regularized Long Wave (RLW) equations:
See Lu et al., An adaptive moving mesh finite element solution of
the Regularized Long Wave equation, Journal of Scientific Computing 74 (2018), 122-144.
(DOI: 10.1007/s10915-017-0427-6) or arXiv:1606.06541.
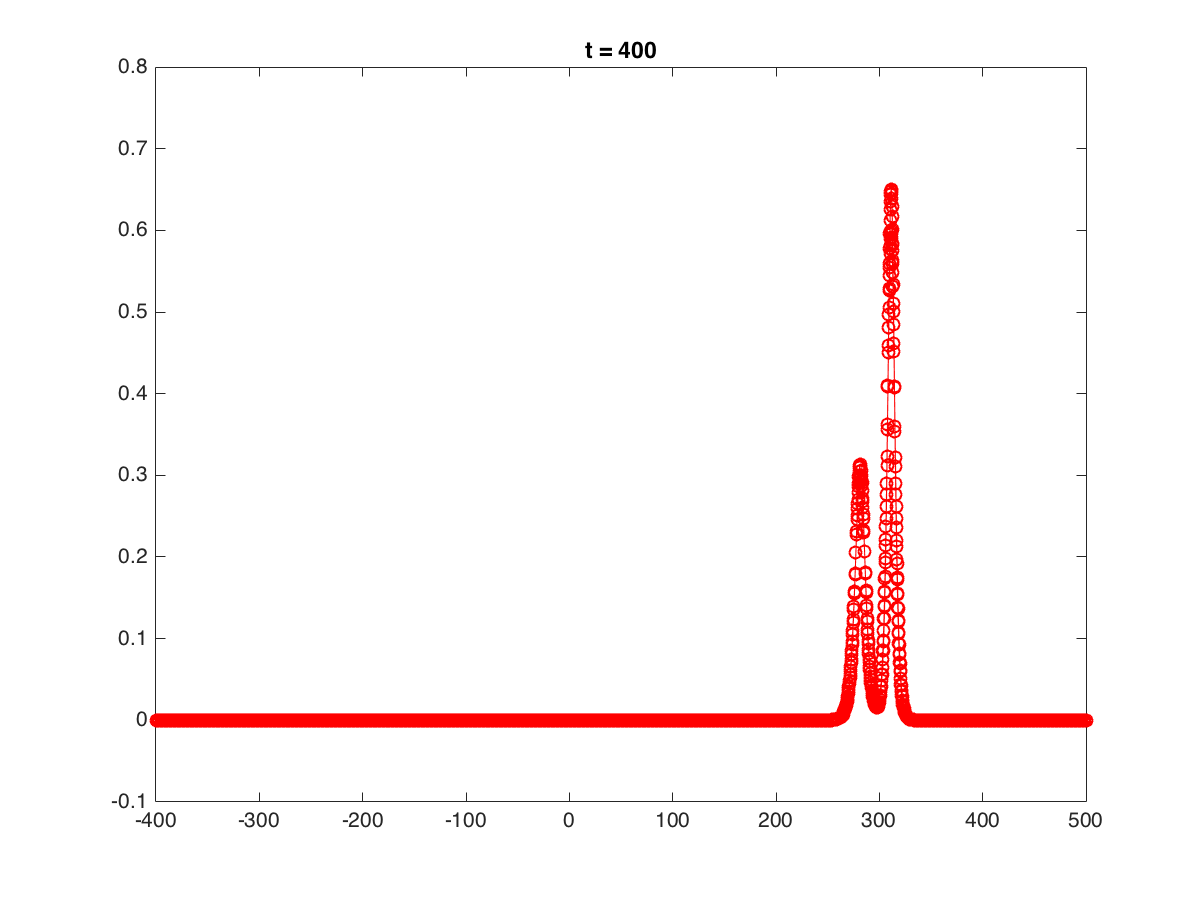
1D: A larger soliton passes by a smaller one. A moving mesh of 800 elements was used on the domain (-400, 500).
|
1D: RLW with the Maxwellian initial solution. A moving mesh of 200 elements was used on the domain (0, 100).
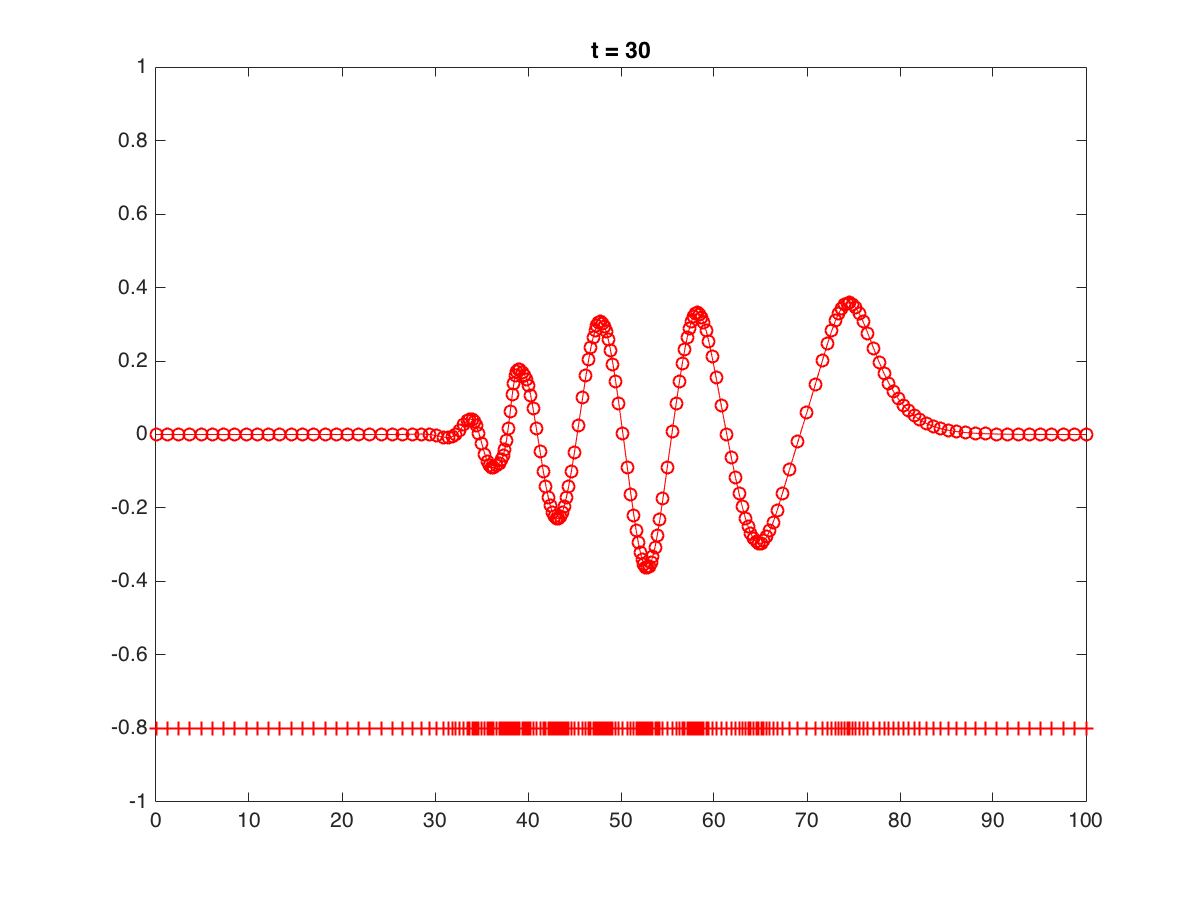
|
1D: RLW with the undularbore initial solution. A moving mesh of 200 elements was used on the domain (-50, 300).
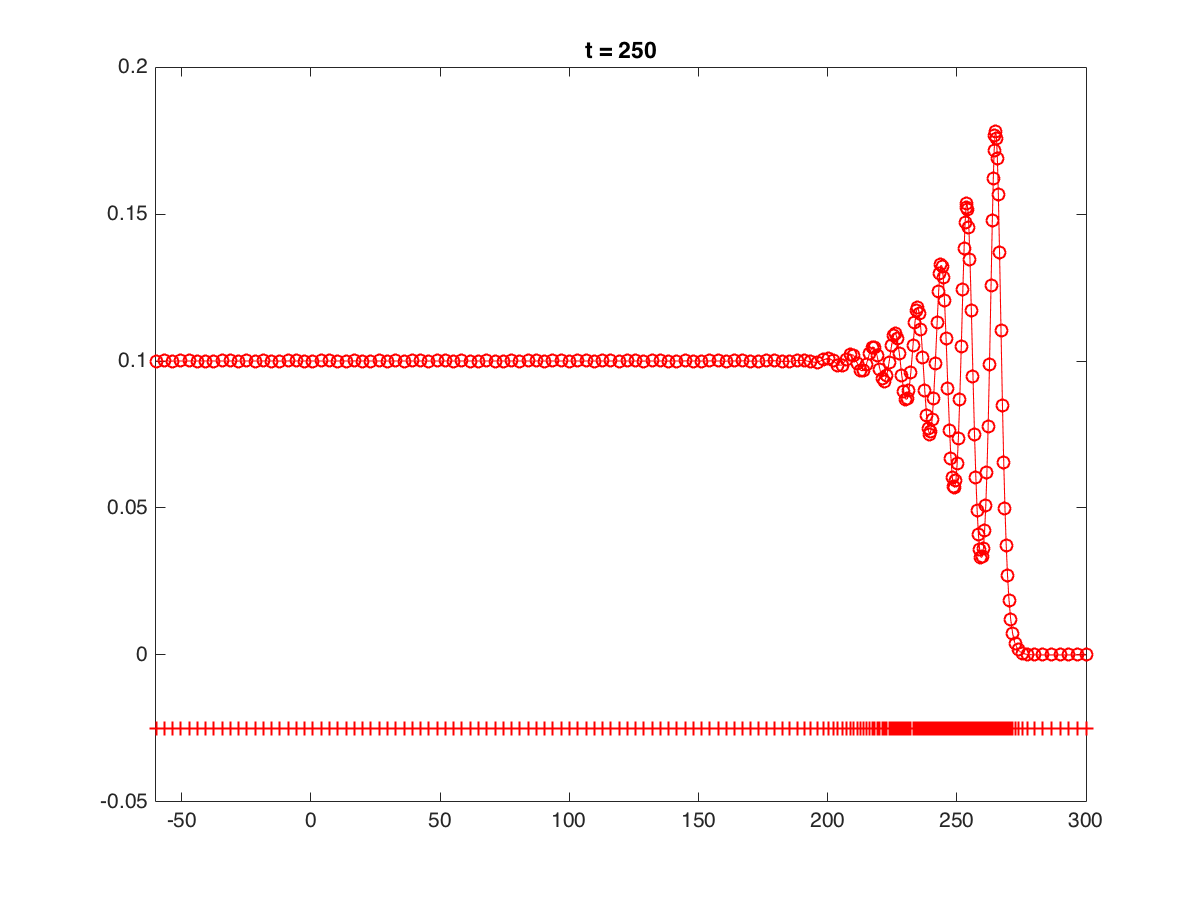
|
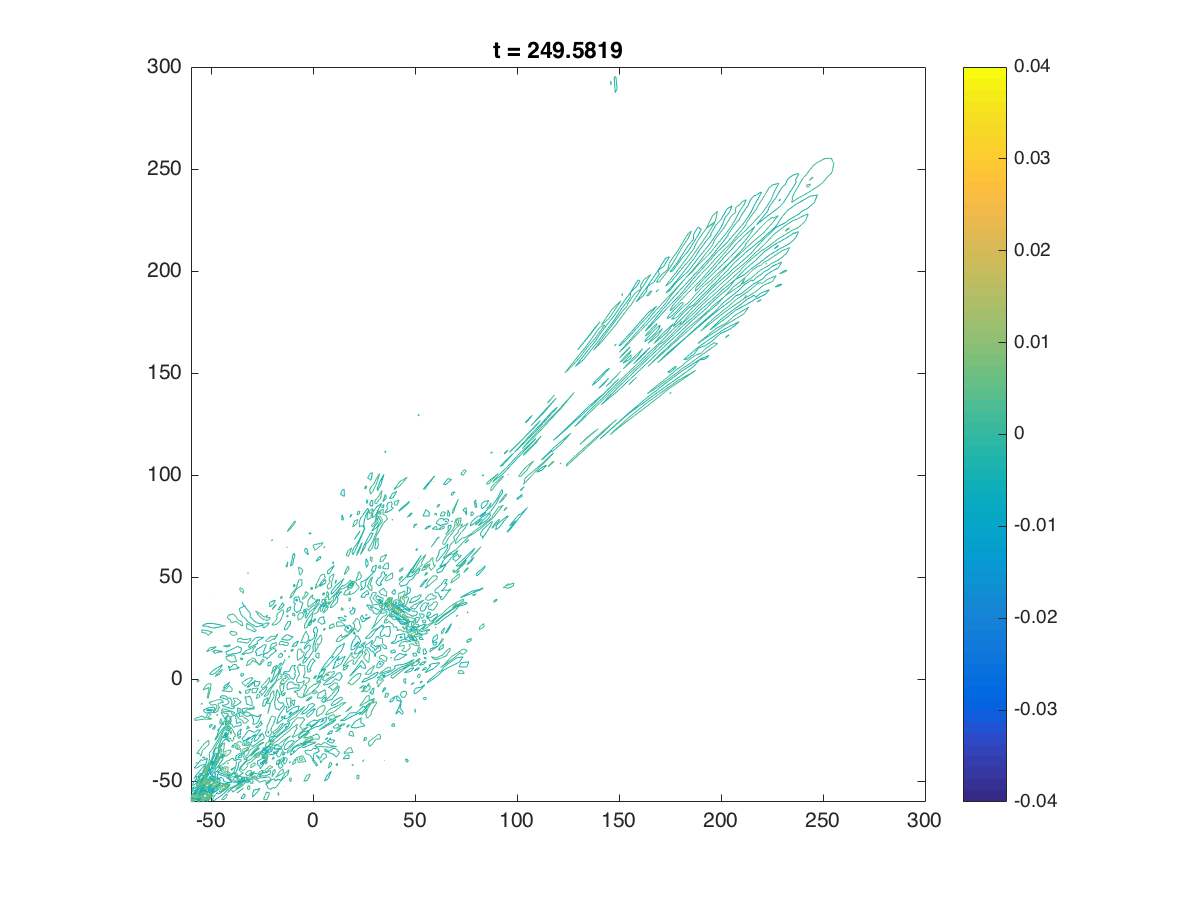
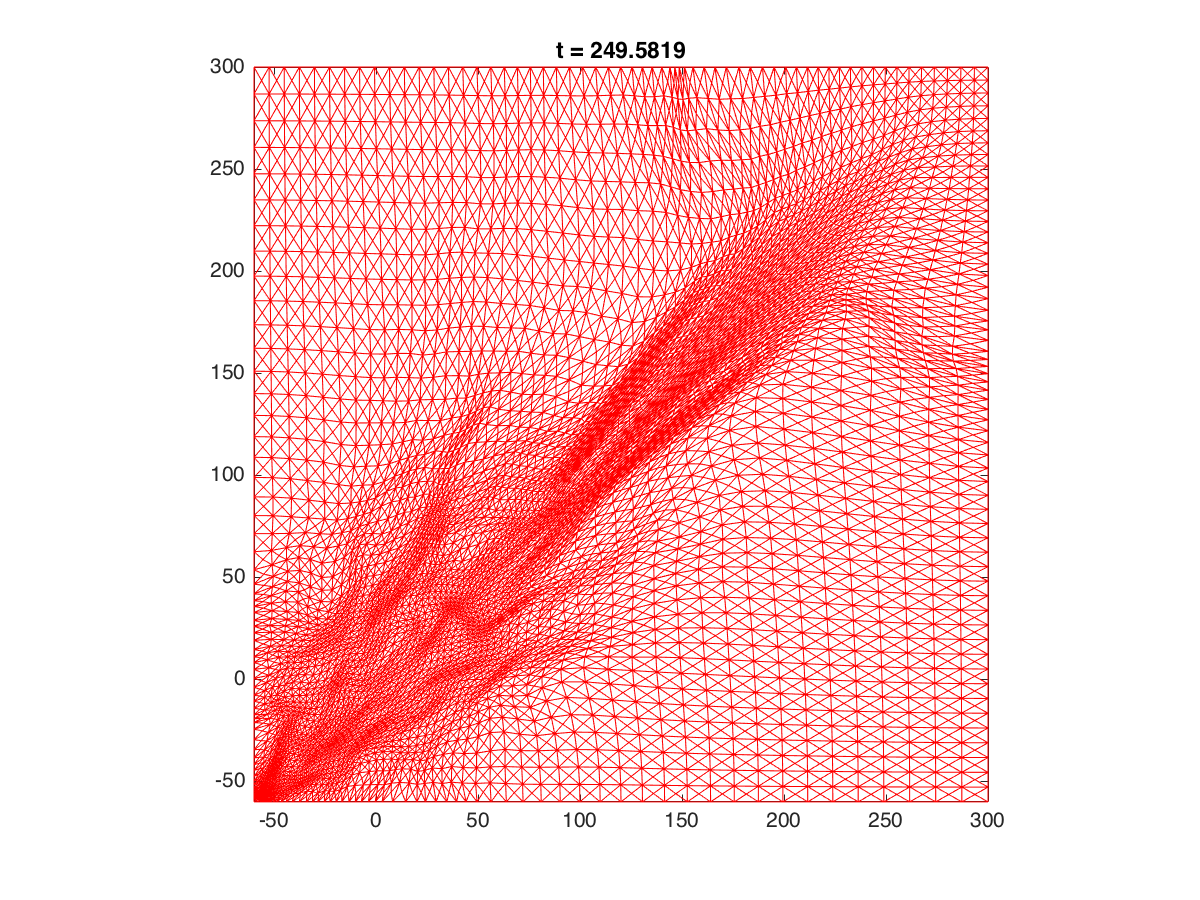
2D: RLW with the undularbore initial solution. A moving mesh of 144000 elements was used
on the domain (-60,300)X(-60,300).
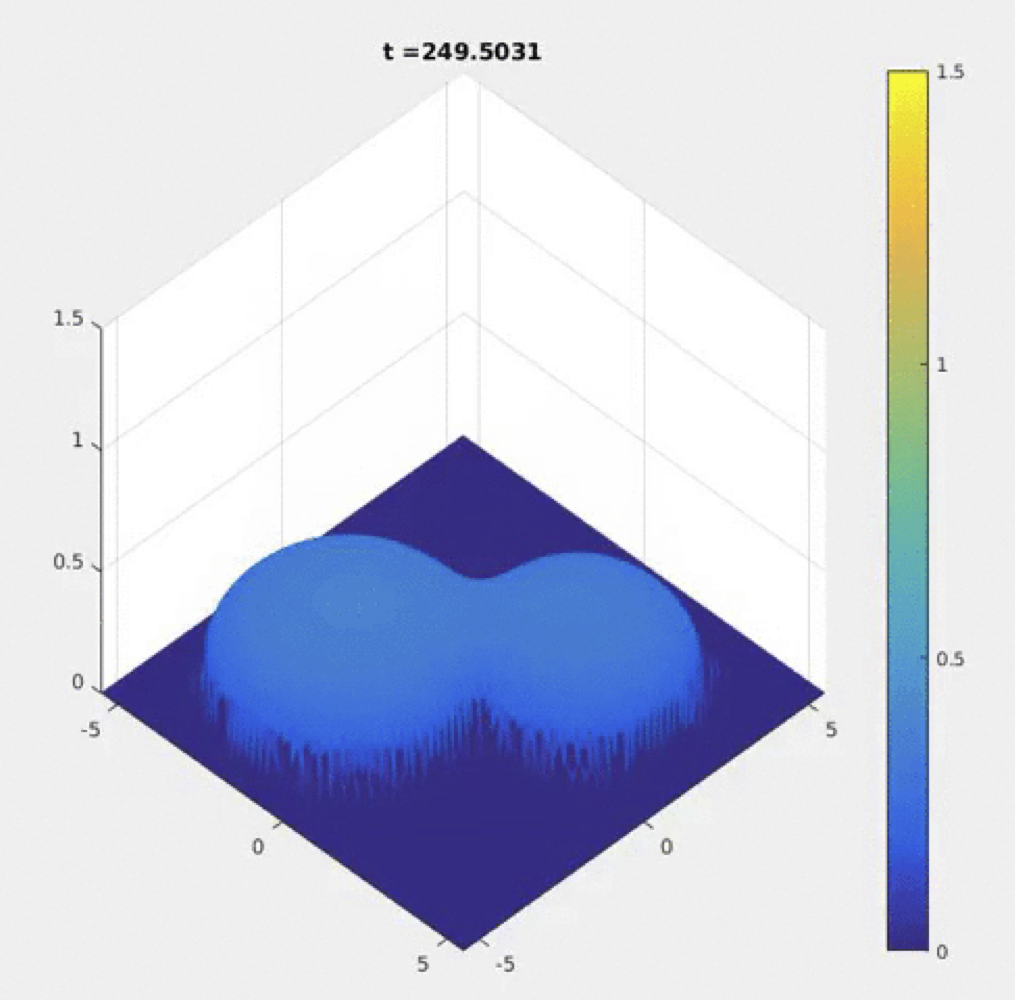
The Porous Medium Equation (PME):
See C. Ngo and W. Huang, A study on moving mesh finite element solution of
the porous medium equation, Journal of Computational Physics 331 (2017), 357-380.
(DOI: 10.1016/j.jcp.2016.11.045) or arXiv:1605.03570.
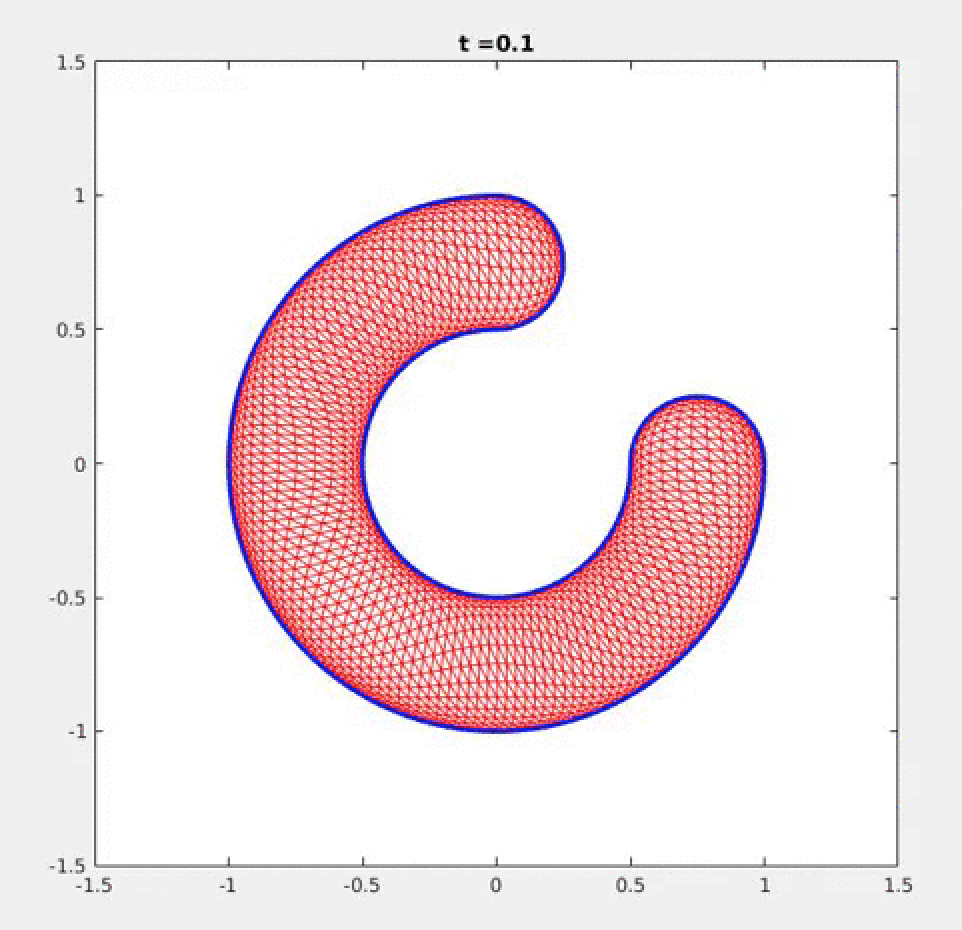
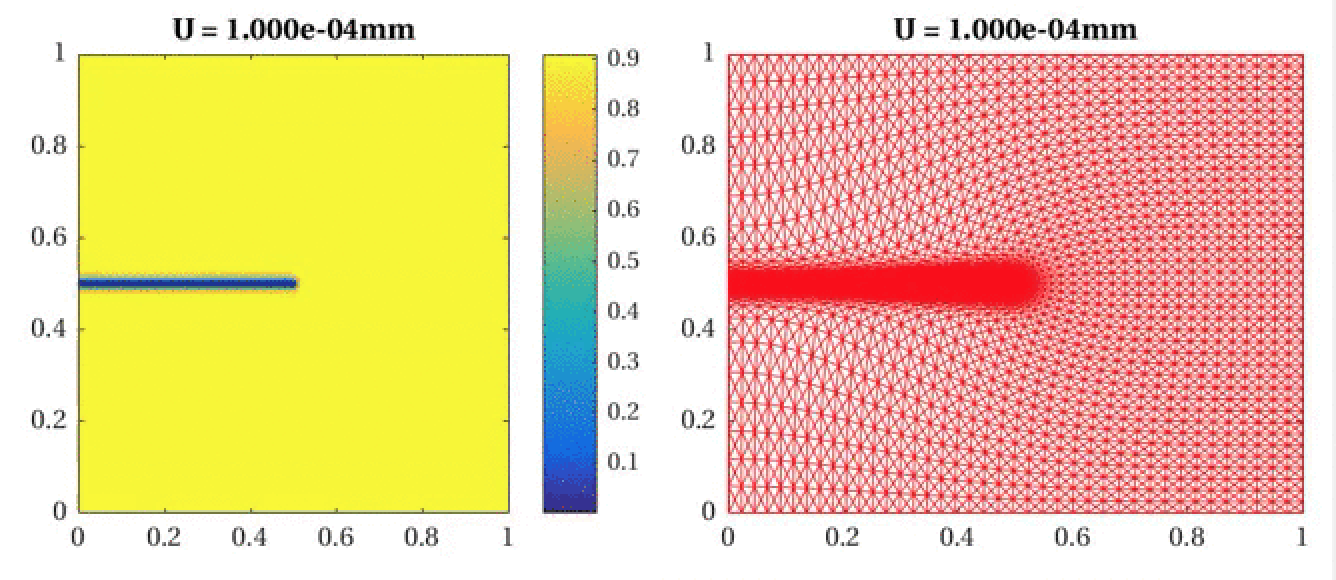
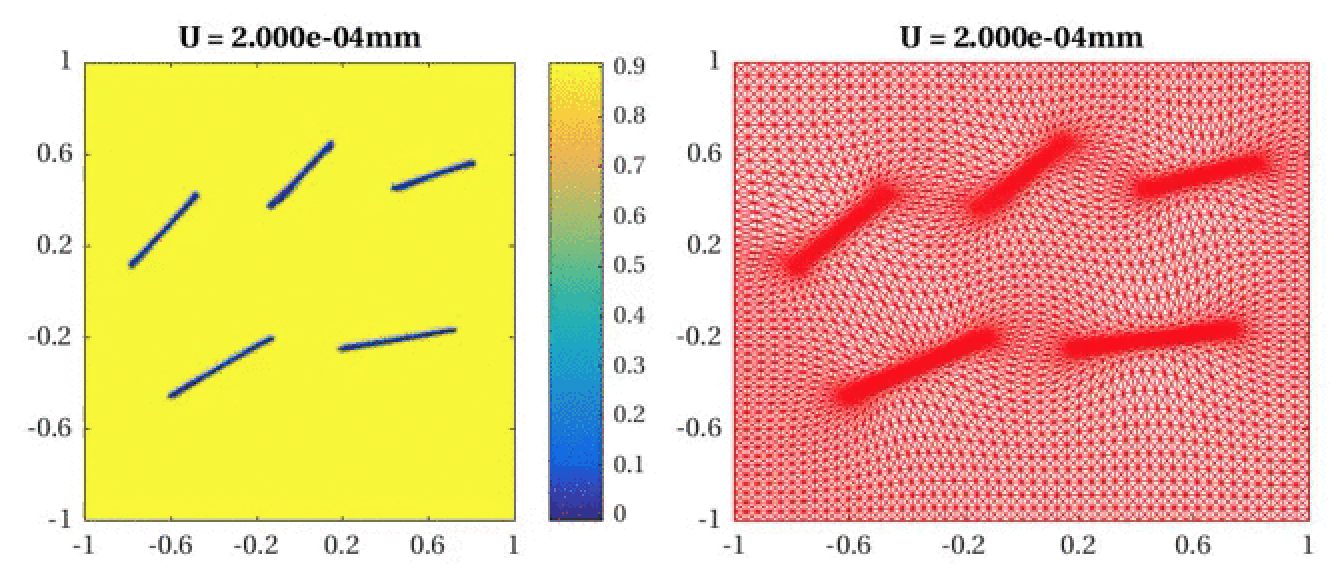
Phase-field modeling of brittle fracture:
See F. Zhang, W. Huang, X. Li, and S. Zhang, Moving Mesh Finite Element Simulation for Phase-Field
Modeling of Brittle Fracture and Convergence of Newton's Iteration, Journal of Computational Physics
356 (2018), 127-149. (DOI: 10.1016/j.jcp.2017.11.033) or (arXiv:1706.05449).